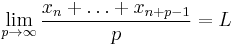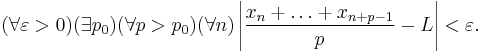Almost convergent sequence

A bounded real sequence 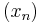$(x_n)$ is said to be almost convergent to $L$ if each Banach limit assigns the same value $L$ to the sequence $(x_n)$ .

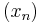Lorentz proved that 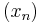$(x_n)$ is almost convergent if and only if

$\lim\limits_{p\to\infty} \frac{x_{n}%2B\ldots%2Bx_{n%2Bp-1}}p=L$

uniformly in $n$ .

The above limit can be rewritten in detail as

$(\forall \varepsilon>0) (\exists p_0) (\forall p>p_0) (\forall n) \left|\frac{x_{n}%2B\ldots%2Bx_{n%2Bp-1}}p-L\right|<\varepsilon.$

Almost convergence is studied in summability theory. It is an example of a summability method which cannot be represented as a matrix method.

References

G. Bennett and N.J. Kalton: "Consistency theorems for almost convergence." Trans. Amer. Math. Soc., 198:23--43, 1974.

J. Boos: "Classical and modern methods in summability." Oxford University Press, New York, 2000.

J. Connor and K.-G. Grosse-Erdmann: "Sequential definitions of continuity for real functions." Rocky Mt. J. Math., 33(1):93--121, 2003.

G.G. Lorentz: "A contribution to the theory of divergent sequences." Acta Math., 80:167--190, 1948.

This article incorporates material from Almost convergent on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.